Après ce grand détour qui nous a appris à penser autrement les valeurs décimales, nous revenons maintenant aux déformations courbes.
Nous les avions laissées [revoir E ce moment] en disant qu'en chaque point nous voulions représenter l'ensemble des sollicitations qui tendent à déplacer ce point dans l'espace. Et nous avions alors admis que ces sollicitations devaient être représentées par un nombre infini de vecteurs, ayant chacun une intensité spécifique, et chacun étant orienté dans une direction spécifique de l'espace.

Pour représenter par un ensemble de vecteurs les sollicitations variées qui forcent un corps à bouger, nous devons donc avoir à notre disposition 3 types distincts de données :
         1/  d'abord nous devons indiquer que, dans ce cas, ce qui arrive au corps matériel  est une déformation de sa position, c'est-à-dire un mouvement dans l'espace. Il aurait pu s'agir d'une autre sorte de déformation : cela aurait pu être une déformation tendant à le percer, ou à l'étirer, ou à faire gonfler son volume, ou à le compresser.
         2/  ensuite, nous devons indiquer l'intensité de cette déformation.
         3/  enfin, nous devons indiquer comment varie cette intensité selon les différentes directions de l'espace.
 

Or, il se trouve que notre analyse de la génération des nombres entiers et décimaux nous a montré qu'un nombre fractionnaire portait nécessairement 3 types différents d'informations :
         1/  la première concerne le nombre entier auquel il est lié.
         2/  la seconde concerne l'ordre séquentiel des déformations successives.
         3/  la dernière, concerne la valeur de cette déformation pour chacune des séquences décimales.
 
 
 

Cela nous suggère un moyen simple pour mesurer une dimension de déformation courbe à laquelle un point est soumis : il suffit d'utiliser un nombre irrationnel. Sa partie entière dira le type de déformation dont il s'agit, et chaque chiffre de la suite décimale portera la valeur d'intensité pour une des directions de l'espace. Ces directions sont en nombre infini mais le nombre des décimales d'un irrationnel l'est également.  Nous viennent alors à l'esprit les dimensions fractales de Mandelbrot.   Et nous nous posons la question : n'est-ce pas exactement cela qu'elles font ? Est-ce qu'elles ne décrivent pas précisément la façon dont un phénomène se déforme, et la façon dont cette déformation varie selon les directions de l'espace ?

 

Envisageons d'abord le chiffre entier qu'elles comportent avant la virgule.

         - 0 -  nous avions commencé à présenter les dimensions de déformation en donnant des exemples de déformations de contrastes. Ainsi, nous avions évoqué la "poussière de Cantor" : un segment dont on a enlevé le 1/3 central, puis enlevé le 1/3 central des 2 segments restants, puis etc., à l'infini.  [revoir E cette figure]
Il se trouve que la dimension fractale d'une telle poussière de Cantor où la déformation n'implique aucun déplacement, est Log 3/ Log 2, c'est-à-dire environ 0,63.
Sa partie entière est donc 0.

         - 1 -  Ainsi que nous le verrons dans les exemples prochains [images ci-dessous], les valeurs fractales des trajets que Mandelbrot indique dans son ouvrage "les objets fractals" [Flammarion - 3ème édition - 1989], se trouvent toutes comprises entre 1 et 2.
C'est-à-dire que leur partie entière est toujours 1.

         - 2 -  Enfin, on constate que la valeur fractale d'une "courbe de Peano" est 2 [Voir F cette figure dans le texte suivant]. Or le principe de cette courbe, est de déformer le découpage d'une surface sur elle- même de telle sorte que change régulièrement la distribution de ses parties blanches et de ses parties colorées, sans cependant que leur proportion réciproque ne soit modifiée. Pour obtenir ce résultat, à chaque stade de son tracé la courbe réalise une division plus tortueuse entre les deux parties de la surface.
Alors on se dit que peut-être la valeur entière 2 dans une dimension fractale a à voir avec la déformation d'un corps sur lui-même.
 
 
 
Quant à la valeur décimale des dimensions fractales, nous savons que la plupart du temps elle correspond à un nombre irrationnel, résultant de la division de deux logarithmes. Ainsi, elle contient bien une suite infinie et ordonnée d'informations.
 
 
 
Il reste à envisager la représentation graphique de ces dimensions.
Mandelbrot donne l'exemple [ouvrage cité ci-dessus d'où son extraits les graphiques] de la dimension fractale  Log 4/Log 3, c'est-à- dire environ 1,2618, pour la courbe en "flocon de neige" de Von Kock. Cette  courbe ne peut pas être réellement dessinée, car elle correspond à un processus infini. On prend un triangle équilatéral. Sur chaque côté du triangle, on construit un triangle équilatéral porté par son 1/3 central. Sur chaque côté des derniers triangles réalisés on construit . . . etc. à l'infini.

 

génération du "flocon de neige" de Von Kock  (à poursuivre à l'infini)

 

le "flocon de neige" de Von Kock  Dimension = Log 34 ~ 1,2318

 
 

Autre exemple : pour une valeur de dimension fractale Log 5/Log 4, c'est-à-dire environ 1,16, on obtient ce genre de courbe que l'on doit aussi poursuivre à l'infini, et dont ne sont représentées ici que les premières étapes.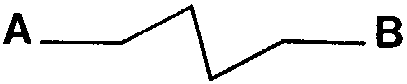

 

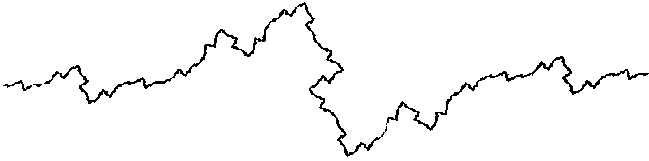Dimension = Log 45 ~ 1,16

 
 
 
 
On remarque tout de suite l'intérêt graphique de la correspondance entre une dimension fractale et de telles courbes.
Pour représenter la valeur d'une force "vectorielle", un vecteur précisément suffisait.
Une courbe fractale n'est pas loin d'avoir la même simplicité qu'un vecteur, car il n'est pas besoin de représenter toute la courbe infinie. Puisque l'on retrouve à toutes les échelles la même courbe et dans tous les détails les mêmes détails, on est dispensé de la représenter en entier. Une seule échelle suffit, et tant qu'à faire autant utiliser la plus grande. Ainsi, dans le cas de la dimension "environ 1,16", le schéma AB suffit pour représenter virtuellement les courbes en nombre infini construites toutes sur le même modèle et à toutes les échelles de détail possibles.
Une question reste cependant posée : de même que l'on peut calculer graphiquement la combinaison de plusieurs forces vectorielles par la résultante de leurs vecteurs, peut-on espérer calculer graphiquement la combinaison de plusieurs déformations courbes par une quelconque construction faite sur leurs courbes fractales ?
On ne fera pas ici de suggestion à ce propos, et la question restera ouverte.
 
 
 
 

Comment retrouver une valeur fixe à la dimension fractale d'un trajet
 

Si maintenant on regarde la courbe AB du dessin précédent, non plus comme une figure dessinée, mais comme le trajet d'un mobile qui va de A jusqu'à B, on se dit que ce type de trajet évoque assez bien ce qui se passe quand un corps est entraîné vers un autre par une déformation courbe : le graphique montre qu'il part de A, arrive à B, et que pour réaliser ce trajet il ne subit pas une attraction uniquement dirigée vers B, mais qu'il est attiré constamment et simultanément dans d'autres directions.
En somme, s'il finit par arriver très exactement sur B et pas à côté, ce n'est que parce que les attractions selon les différentes directions de l'espace sont bien combinées entre elles, et qu'elles le sont à toutes les échelles du trajet.
 

Il y a cependant une objection majeure que fait Mandelbrot lui-même, à l'utilisation des courbes fractales comme représentation valide d'un trajet suivi par un mobile. Cette objection a trait à la longueur du trajet.
En effet, si on calcule la longueur d'une courbe fractale, on s'aperçoit qu'elle est infinie. Pour la dessiner, chaque fois que l'on descend d'un cran dans l'échelle de détail de son parcours, on transforme un segment droit en une série de segments qui ondulent sur ce 1er segment. Comme la droite est le plus court chemin entre deux points, chaque étape dans le "raffinement du détail" a donc pour effet de rallonger la courbe. Certaines suites infinies convergent vers une somme finie, mais ici ce n'est pas le cas car le facteur de rallongement du parcours est constant et ne diminue pas avec l'échelle de détail.
Si la courbe est de longueur infinie, il ne semble donc pas possible de l'utiliser pour mesurer le trajet parfaitement fini réalisé par un mobile.
Pour éviter d'obtenir ce résultat de longueur infinie, on peut décider de ne pas dessiner la courbe dans tous ses infinis détails et s'arrêter à un moment donné dans la cascade de sa génération. Mais alors, selon le degré de détail que l'on prend en compte, c'est-à-dire  selon l'échelle de détails jusqu'à laquelle on descend, la longueur du trajet obtenu est chaque fois différente.
 
 

Le trajet fractal serait donc soit de longueur infinie, soit de longueur finie mais variable avec l'échelle de sa mesure ? Une courbe fractale semble ainsi bien mal partie pour servir à représenter le trajet d'un mobile entraîné par une déformation courbe.  Cette fois encore, l'analyse que l'on a fait plus haut des nombres décimaux va nous servir à comprendre où réside l'anomalie.

On a dit qu'un nombre décimal porte 3 informations, qu'il est donc équivalent à un espace 3 D, c'est-à-dire un volume. Or, on ne veut avoir ici qu'une longueur de trajet, qui est une donnée 1 D.
Si par exemple nous avons un problème du genre : "le volume d'un corps parallélépipédique est de 1,26 m3, quelle est sa longueur ?", nous savons que nous ne pouvons pas le résoudre. La valeur 1,26 a bien été obtenue en multipliant une longueur par une largeur et une hauteur. Mais en sens inverse, nous ne pouvons pas retrouver ces 3 données, qui sont  pourtant "contenues" dans la valeur du volume. Pour trouver la longueur, nous devons d'abord "dégonfler" le volume en donnant la hauteur, puis le "déplatir" en donnant sa largeur.
De la même façon, pour calculer la longueur d'un trajet fractal, il faut redonner avant calcul les 2 informations que la dimension fractale a "mélangées" avec la longueur du trajet : la dimension en ligne droite entre les deux points extrêmes du trajet, et l'échelle de détail à laquelle on effectue le trajet, choisie parmi le nombre infini des échelles possibles.
L'anomalie de la longueur infinie des courbes fractales réside simplement dans le fait que l'on veut utiliser "toute" la dimension fractale pour calculer la longueur d'un trajet, alors qu'une dimension fractale porte "trop" d'informations pour cela : il faut la "dégonfler" puis la "déplatir" pour trouver la longueur qu'elle contient.

Concernant cet aspect des dimensions fractales, nous divergeons donc de la présentation qu'en a fait Mandelbrot. À la question : "quelle est la longueur de la côte de la Bretagne ?", Mandelbrot répond : elle est de longueur infinie car nous pouvons toujours la suivre sur une échelle plus petite. Le trajet peut être fait en voiture, ou fait à pied pour en suivre mieux les méandres, ou au pas d'une souris, ou peut contourner tous ses grains de sable, ou peut contourner tous les atomes qui en marquent la limite : à chaque cran de précision la longueur du trajet se rapprochera de l'infini. À la même question, nous répondons ici : la côte bretonne a toujours une longueur finie, mais elle a un nombre infini de longueurs, chacune correspondant à l'échelle de mesure que l'on choisit, parmi le nombre infini des échelles de mesure possibles.
 
 

Dans un système de mesure par coordonnées, un trajet ne possède qu'une seule longueur.      Dans un système de mesure par dimensions de déformation, un trajet possède un nombre infini de longueurs qui sont toutes résumées par un seul nombre.      Par conséquent, une dimension fractale contient infiniment plus d'informations qu'une dimension de coordonnées, et demande seulement qu'on lui dise lequel de ces trajets l'on veut. Quand on a répondu à sa demande, elle nous en fournit la longueur.